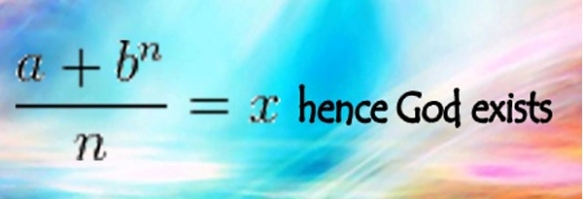Kurt Gödel Offers Proof of the Existence of God
The first version of the ontological proof in Gödel’s papers is dated “around 1941”. Gödel is not known to have told anyone about his work on the proof until 1970, when he thought he was dying. In February, he allowed Dana Scott to copy out a version of the proof, which circulated privately. In August 1970, Gödel told Oskar Morgenstern that he was “satisfied” with the proof, but Morgenstern recorded in his diary entry for 29 August 1970, that Gödel would not publish because he was afraid that others might think “that he actually believes in God, whereas he is only engaged in a logical investigation (that is, in showing that such a proof with classical assumptions (completeness, etc.) correspondingly axiomatized, is possible).”[2]Gödel died January 14, 1978. Another version, slightly different from Scott’s, was found in his papers. It was finally published, together with Scott’s version, in 1987.[3]
Morgenstern’s diary is an important and usually reliable source for Gödel’s later years, but the implication of the August 1970 diary entry—that Gödel did not believe in God—is not consistent with the other evidence. In letters to his mother, who was not a churchgoer and had raised Kurt and his brother as freethinkers,[4] Gödel argued at length for a belief in an afterlife.[5] He did the same in an interview with a skeptical Hao Wang, who said: “I expressed my doubts as G spoke […] Gödel smiled as he replied to my questions, obviously aware that his answers were not convincing me.”[6] Wang reports that Gödel’s wife, Adele, two days after Gödel’s death, told Wang that “Gödel, although he did not go to church, was religious and read the Bible in bed every Sunday morning.”[7] In an unmailed answer to a questionnaire, Gödel described his religion as “baptized Lutheran (but not member of any religious congregation). My belief is theistic, not pantheistic, following Leibnizrather than Spinoza.”[8]
The proof uses modal logic, which distinguishes between necessary truths and contingent truths. In the most common semantics for modal logic, many “possible worlds” are considered. A truth is necessary if it is true in all possible worlds. By contrast, a truth is contingent if it just happens to be the case, for instance, “more than half of the planet is covered by water”. If a statement happens to be true in our world, but is false in another world, then it is a contingent truth. A statement that is true in some world (not necessarily our own) is called a possible truth.
From axioms 1 through 4, Gödel argued that in some possible world there exists God. He used a sort of modal plenitude principle to argue this from the logical consistency of Godlikeness. Note that this property is itself positive, since it is the conjunction of the (infinitely many) positive properties.
Then, Gödel defined essences: if x is an object in some world, then the property P is said to be an essence of x if P(x) is true in that world and if P entails all other properties that x has in that world. We also say that x necessarily exists if for every essence P the following is true: in every possible world, there is an element y with P(y).
Since necessary existence is positive, it must follow from Godlikeness. Moreover, Godlikeness is an essence of God, since it entails all positive properties, and any nonpositive property is the negation of some positive property, so God cannot have any nonpositive properties. Since any Godlike object is necessarily existent, it follows that any Godlike object in one world is a Godlike object in all worlds, by the definition of necessary existence. Given the existence of a Godlike object in one world, proven above, we may conclude that there is a Godlike object in every possible world, as required.
From these hypotheses, it is also possible to prove that there is only one God in each world by Leibniz’s law, the identity of indiscernibles: two or more objects are identical (are one and the same) if they have all their properties in common, and so, there would only be one object in each world that possesses property G. Gödel did not attempt to do so however, as he purposely limited his proof to the issue of existence, rather than uniqueness. This was more to preserve the logical precision of the argument than due to a penchant for polytheism. This uniqueness proof will only work if one supposes that the positiveness of a property is independent of the object to which it is applied, a claim which some have considered to be suspect[who?].
To formalize the argument sketched above, the following definitions and axioms are needed:
-
Definition 1: x is God-like if and only if x has as essential properties those and only those properties which are positive
-
Definition 2: A is an essence of x if and only if for every property B, x has B necessarily if and only if A entails B
-
Definition 3: x necessarily exists if and only if every essence of x is necessarily exemplified
-
Axiom 1: Any property entailed by—i.e., strictly implied by—a positive property is positive
-
Axiom 2: A property is positive if and only if its negation is not positive
-
Axiom 3: The property of being God-like is positive
-
Axiom 4: If a property is positive, then it is necessarily positive
-
Axiom 5: Necessary existence is a positive property
Axiom 1 assumes that it is possible to single out positive properties from among all properties. Gödel comments that “Positive means positive in the moral aesthetic sense (independently of the accidental structure of the world)… It may also mean pure attribution as opposed to privation (or containing privation).” (Gödel 1995). Axioms 2, 3 and 4 can be summarized by saying that positive properties form a principal ultrafilter.
From these axioms and definitions and a few other axioms from modal logic, the following theorems can be proved:
-
Theorem 1: If a property is positive, then it is consistent, i.e., possibly exemplified.
-
Theorem 2: The property of being God-like is consistent.
-
Theorem 3: If something is God-like, then the property of being God-like is an essence of that thing.
-
Theorem 4: Necessarily, the property of being God-like is exemplified.
Symbolically:
![\begin{array}{rl}\text{Ax. 1.} & \left\{P(\varphi) \wedge \Box \; \forall x[\varphi(x) \to \psi(x)]\right\} \to P(\psi) \\\text{Ax. 2.} & P(\neg \varphi) \leftrightarrow \neg P(\varphi) \\\text{Th. 1.} & P(\varphi) \to \Diamond \; \exists x[\varphi(x)] \\\text{Df. 1.} & G(x) \iff \forall \varphi [P(\varphi) \to \varphi(x)] \\\text{Ax. 3.} & P(G) \\\text{Th. 2.} & \Diamond \; \exists x \; G(x) \\\text{Df. 2.} & \varphi \text{ ess } x \iff \varphi(x) \wedge \forall \psi \left\{\psi(x) \to \Box \; \forall y[\varphi(y) \to \psi(y)]\right\} \\\text{Ax. 4.} & P(\varphi) \to \Box \; P(\varphi) \\\text{Th. 3.} & G(x) \to G \text{ ess } x \\ \text{Df. 3.} & E(x) \iff \forall \varphi[\varphi \text{ ess } x \to \Box \; \exists y \; \varphi(y)] \\ \text{Ax. 5.} & P(E) \\ \text{Th. 4.} & \Box \; \exists x \; G(x) \end{array}](https://i0.wp.com/upload.wikimedia.org/math/a/b/4/ab47f643c7918fda58089c7f5129a183.png)
There is an ongoing open-source effort to formalize Gödel’s proof using various theorem provers and proof assistants. The formalized proof of God’s existence made headlines in German newspapers.
__________________________________________________________

ABC NEWS
Computer Scientists ‘Prove’ God Exists
Oct. 27, 2013
By David Knight, SPIEGEL
Two scientists have formalized a theorem regarding the existence of God penned by mathematician Kurt Gödel. But the God angle is somewhat of a red herring — the real step forward is the example it sets of how computers can make scientific progress simpler.
As headlines go, it’s certainly an eye-catching one. “Scientists Prove Existence of God,” German daily Die Welt wrote last week.
But unsurprisingly, there is a rather significant caveat to that claim. In fact, what the researchers in question say they have actually proven is a theorem put forward by renowned Austrian mathematician Kurt Gödel — and the real news isn’t about a Supreme Being, but rather what can now be achieved in scientific fields using superior technology.
When Gödel died in 1978, he left behind a tantalizing theory based on principles of modal logic — that a higher being must exist. The details of the mathematics involved in Gödel’s ontological proof are complicated, but in essence the Austrian was arguing that, by definition, God is that for which no greater can be conceived. And while God exists in the understanding of the concept, we could conceive of him as greater if he existed in reality. Therefore, he must exist.
Even at the time, the argument was not exactly a new one. For centuries, many have tried to use this kind of abstract reasoning to prove the possibility or necessity of the existence of God. But the mathematical model composed by Gödel proposed a proof of the idea. Its theorems and axioms — assumptions which cannot be proven — can be expressed as mathematical equations. And that means they can be proven.
Proving God’s Existence with a MacBook
That is where Christoph Benzmüller of Berlin’s Free University and his colleague, Bruno Woltzenlogel Paleo of the Technical University in Vienna, come in. Using an ordinary MacBook computer, they have shown that Gödel’s proof was correct — at least on a mathematical level — by way of higher modal logic. Their initial submission on the arXiv.org research article server is called “Formalization, Mechanization and Automation of Gödel’s Proof of God’s Existence.”
The fact that formalizing such complicated theorems can be left to computers opens up all kinds of possibilities, Benzmüller told SPIEGEL ONLINE. “It’s totally amazing that from this argument led by Gödel, all this stuff can be proven automatically in a few seconds or even less on a standard notebook,” he said.
The name Gödel may not mean much to some, but among scientists he enjoys a reputation similar to the likes of Albert Einstein — who was a close friend. Born in 1906 in what was then Austria-Hungary and is now the Czech city of Brno, Gödel later studied in Vienna before moving to the United States after World War II broke out to work at Princeton, where Einstein was also based. The first version of this ontological proof is from notes dated around 1941, but it was not until the early 1970s, when Gödel feared that he might die, that it first became public.
Now Benzmüller hopes that using such a headline-friendly example can help draw attention to the method. “I didn’t know it would create such a huge public interest but (Gödel’s ontological proof) was definitely a better example than something inaccessible in mathematics or artificial intelligence,” the scientist added. “It’s a very small, crisp thing, because we are just dealing with six axioms in a little theorem. … There might be other things that use similar logic. Can we develop computer systems to check each single step and make sure they are now right?”
‘An Ambitious Expressive Logic’
The scientists, who have been working together since the beginning of the year, believe their work could have many practical applications in areas such as artificial intelligence and the verification of software and hardware.
Benzmüller also pointed out that there are many scientists working on similar subject areas. He himself was inspired to tackle the topic by a book entitled “Types, Tableaus and Gödel’s God,” by Melvin Fitting.
The use of computers to reduce the burden on mathematicians is not new, even if it is not welcomed by all in the field. American mathematician Doron Zeilberger has been listing the name Shalosh B. Ekhad on his scientific papers since the 1980s. According to the New York-based Simons Foundation, the name is actually a pseudonym for the computers he uses to help prove theorems in seconds that previously required page after page of mathematical reasoning. Zeilberger says he gave the computer a human-sounding name “to make a statement that computers should get credit where credit is due.” “human-centric bigotry” on the part of mathematicians, he says, has limited progress.
Ultimately, the formalization of Gödel’s ontological proof is unlikely to win over many atheists, nor is it likely to comfort true believers, who might argue the idea of a higher power is one that defies logic by definition. For mathematicians looking for ways to break new ground, however, the news could represent an answer to their prayers.
link athttp://abcnews.go.com/Technology/computer-scientists-prove-god-exists/story?id=20678984
__________________________________________________________
Leonhard Euler Offers Proof of the Existence of God
Leonhard Euler (April 15,1707 – September 18, 1783) was a pioneering Swiss mathematician and physicist who made important discoveries in fields as diverse as infinitesimal calculus and graph theory. Euler also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function, and he is renowned for his work in mechanics, fluid dynamics, optics, and astronomy. He spent most of his adult life in St. Petersburg, Russia and in Berlin, Prussia.
Much of what is known of Euler’s religious beliefs can be deduced from his Letters to a German Princess and an earlier work, Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister (Defense of the Divine Revelation against the Objections of the Freethinkers). These works show that Euler was a devout Christian who believed the Bible to be inspired; the Rettung was primarily an argument for the divine inspiration of scripture.
There is a famous legend inspired by Euler’s arguments with secular philosophers over religion, which is set during Euler’s second stint at the St. Petersburg academy. The French philosopher Denis Diderot was visiting Russia on Catherine the Great’s invitation. However, the Empress was alarmed that the philosopher’s arguments for atheism were influencing members of her court, so Euler was asked to confront the Frenchman. Diderot was informed that a learned mathematician had produced a proof of the existence of God; he agreed to view the proof as it was presented in court. Euler appeared, advanced toward Diderot, and in a tone of perfect conviction announced the following non-sequitur: “Sir, \frac{a+b^n}{n}=x, hence God exists—reply!” Diderot, to whom (says the story) all mathematics was gibberish, stood dumbstruck as peals of laughter erupted from the court. Embarrassed, he asked to leave Russia, a request that was graciously granted by the Empress.
link athttp://www.oddee.com/item_98822.aspx
__________________________________________________________
Mathematicians and scientists seemed to ignore a simple equation familiar to all grammar school children: 0 + 0 = 0
For the Big Bang Theory to work, this always-true equation had to be false—at least once—and if this basic equation is unreliable, so is the rest of the math used to prove the Big Bang.
Dr. Adrian Rogers, a pastor and Bible teacher from Memphis, TN, once challenged the Big Bang Theory by putting the 0 + 0 = 0 equation into more specific terms: “How can nobody plus nothing equal everything?”
__________________________________________________________
A Proof Even Better Than Math
I’m no math expert, but for more than 40 years I have studied how people act and why they do what they do. Human nature is remarkably consistent, regardless of the culture or era in history. For me, the best proof of God depends on one cowardly fisherman.
Simon Peter, Jesus’ closest friend, denied knowing Jesus three times in the hours before the crucifixion. If any of us had faced possible crucifixion, we probably would have done the same thing. Peter’s so-called cowardice was completely predictable. It was human nature.
But it was what happened later that causes me to believe. Not only did Peter come out of hiding after Jesus’ death, he began preaching the resurrection of Christ so loudly that the authorities threw him in jail and had him severely beaten. But he got out and preached all the more!
And Peter wasn’t alone. All the apostles who had been cowering behind locked doors spread out across Jerusalem and the surrounding area and began insisting that the Messiah had been raised from the dead. In the following years, all of Jesus’ apostles (except Judas who hanged himself and John, who died of old age) were so fearless in proclaiming the gospel that they were all murdered as martyrs.
That is simply not human nature.
One thing and one thing only can explain it: These men had encountered the real, solid, bodily-resurrected Jesus Christ. Not a hallucination. Not mass hypnosis. Not looking in the wrong tomb or any other silly excuse. The flesh and blood risen Christ.
That’s what my father believed and that’s what I believe. I don’t have to do the math to know that my Savior lives, and because He lives, I fully expect to see both Him and my father again some day.
link athttp://christianity.about.com/od/newchristians/a/proofgodexists.htm
__________________________________________________________
POSITIVE PROOF OF GOD”S EXISTENCE!!!
I have met him, he loves me and he lives within me!